Definitions
Following the definitions laid out in (Richeson 2010), an (\(n\)-1)-dimensional sphere1 of radius \(r\) is the set of points in Euclidean \(n\)-dimensional space \(\mathbb{R}^{n}\) satisfying \(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=r^{2}\).
The region enclosed by an \((n-1)\)-sphere is sometimes called an \(n\)-dimensional ball (or \(n\)-ball). It is the set of points in \(\mathbb{R}^{n}\) satisfying \(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\le r^{2}\).
Sphere is one dimension less than the enclosed \(n\)-ball because it is a surface embedded in \(\mathbb{R}^{n}\).
Surface Area and Volume
The surface area and volume of an \((n-1)\)-dimensional sphere are given by
\[ S_{n-1}(r)={\frac {2\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2}\right)}} r^{n-1} \] \[ V_{n}(r)={\frac {\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2} + 1\right)}} r^{n} \] Where the Gamma function is a generalization of the factorial function to non-integer numbers. This is the most general form, but there is also a recursive definition. Derivations of this formula can be found in (Rozman 2017) and (Huber 1982).
One well known, yet counter-intuitive phenomenon is how the volume of the sphere changes with the number of dimensions. Let’s consider the unit sphere (a sphere with \(r=1\)). By substituting \(r\) with 1 we obtain:
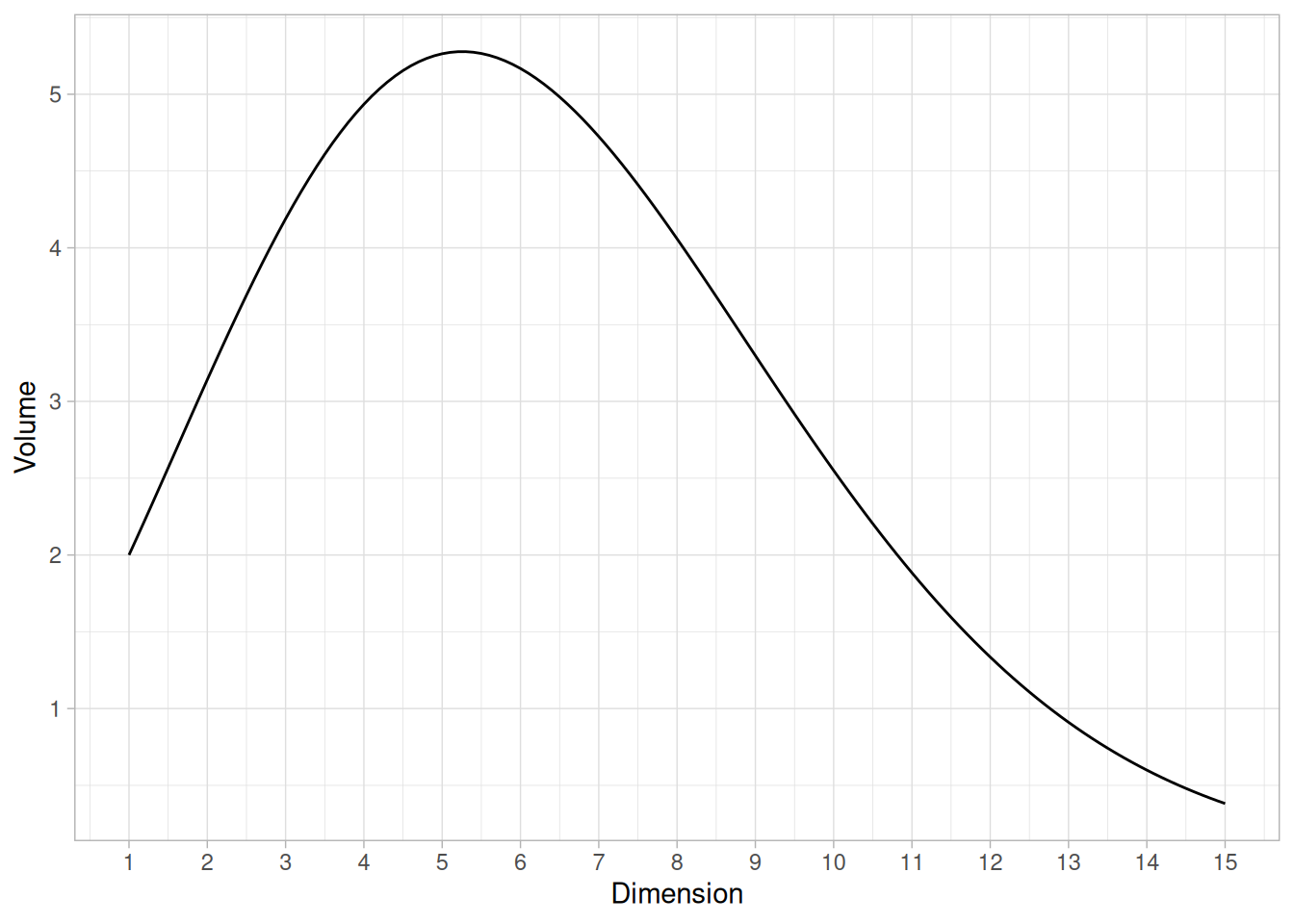
\[ v_n={\frac {\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2} + 1\right)}} \] Many sources would accompany this formula with a graph like this:
A few observations can be made here. First, the volume grows with the number of dimensions, then–quite unexpectedly–it maxes out at about five dimensions, then gradually drops, and apparently goes to zero at infinity2.
\[ \lim_{n \to \infty}{\frac {\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2} + 1\right)}} = 0 \]
This means that the volume of the unit sphere in an infinitely-dimensional space is zero - another surprising result. But does it make sense?
Volume Units
It is unfortunate that the sphere volume formula yields not just some abstract volume, but rather a set of very concrete hyper-volumes, all in different units, one per each value of \(n\). Indeed, comparing 1-volume to 3-volume is the same as comparing say decimeters to liters, and wondering why one is larger than other.
To meaningfully compare volumes we need to get rid of the volume units. There are many ways of achieving it. For example, we can do this by finding a ratio of the sphere’s volume to some other standard volume, such as of the unit cube. One problem here is that it would be difficult to ascribe some kind of physical meaning to the resulting value.
Sphere Packing
A more interesting approach would be finding a proportion of the volume taken by a sphere from the cube enclosing that sphere. Its meaning is straightforward: we pack a sphere into a box and observe what part of the box’ volume it takes. This proportion can be described as
\[ \begin{aligned} p_n(r) &= {\frac {\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2} + 1\right)}} r^{n} \cdot \frac {1} {(2 r)^n} \\ &= \frac {\pi^{\frac {n}{2}}}{2^n \Gamma\left(\frac{n}{2}+1\right) } \end{aligned} \] Where \((2r)^n\) is the total volume of the container, and \(p_n(r)\) is the proportion of the “unused” packing volume. Note how radius \(r\) gets cancelled out, and what is left depends only on \(n\).
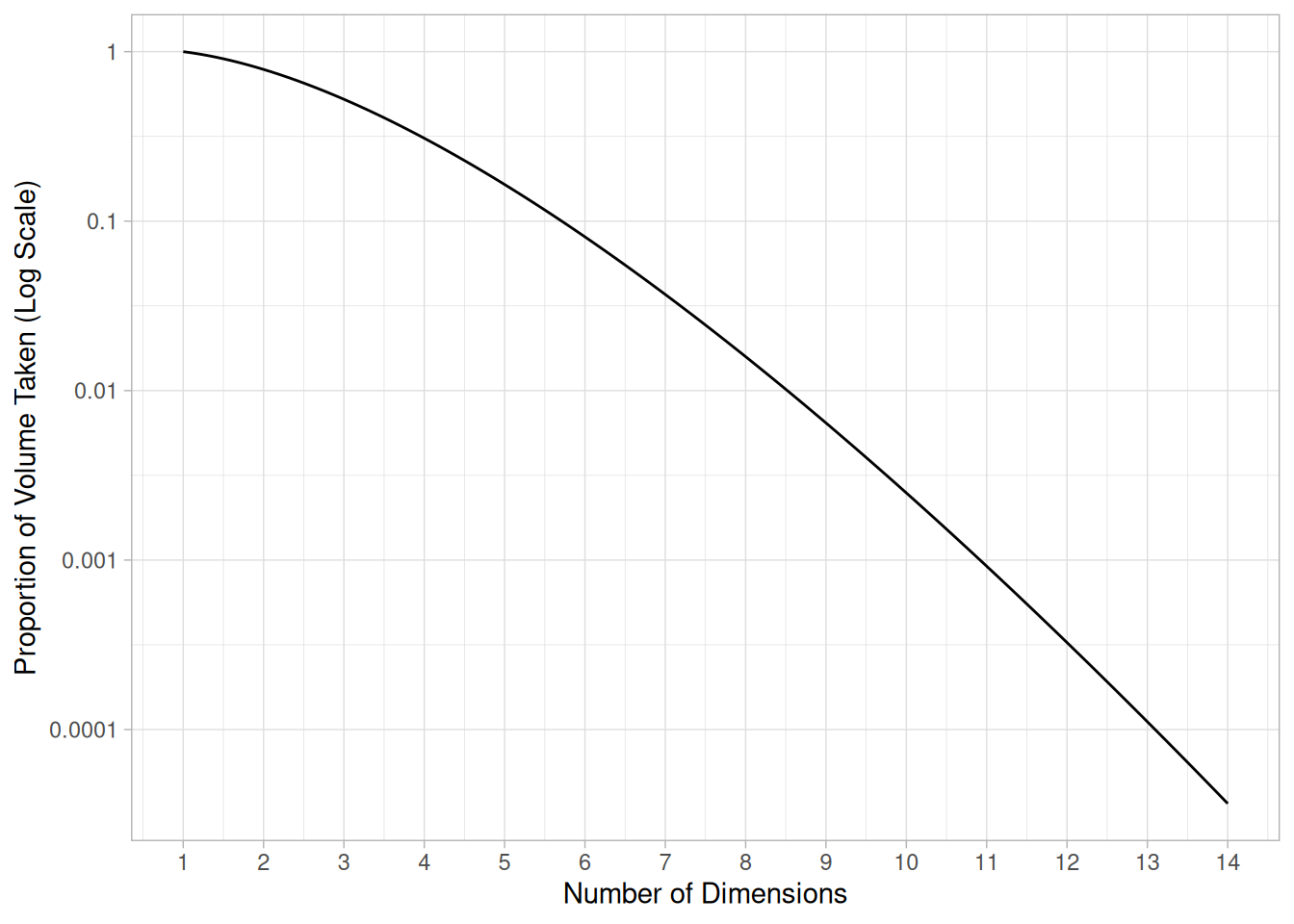
A 1-dimensional “sphere” perfectly fits a 1-dimensional “box.” They are, in fact, the same. On a plane, a circle covers exactly \(\pi/4\) of the area of the enclosing square. At \(n=9\) the volume taken by the sphere is less than 1% of the total volume of the box. In this light we can see that there is nothing special about \(n=5\).
Surface Area to Volume Ratio
Yet another way of looking at the same phenomenon is the surface-to-volume ratio. A sphere is a surface containing a volume. The dimensionality of this surface is one degree less than the volume. If we consider a 3-ball, its surface (sphere) would be two-dimensional. Indeed, each point on the ball’s surface can be described by only two parameters: the rotation angle and the elevation angle.
Surface area and the volume of a sphere are related as
\[ \begin{aligned} \frac{S_{n-1}(r)}{V_{n}(r)} &= {\frac {2\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2}\right)}} r^{n-1} : {\frac {\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2} + 1\right)}} r^{n} \\ &= \frac{2 \Gamma(\frac{n}{2} + 1)}{r\Gamma(\frac{n}{2})} \\ &= \frac{n}{r} \end{aligned} \]
That is, in a space with a given number of dimensions, the larger the radius, the smaller this ratio is.
One practical consequence of this rule is the effect of the size of a living organism on its metabolism. Smaller animals lose more heat (relatively to their mass), so they have to maintain faster metabolism to compensate for the heat loss, and consequently - eat more. Similarly, hypothetical animals living in higher dimensional spaces would also have to eat more, proportionally to the number of dimensions.
Appendix 1
The volume of the unit \(n\)-sphere is given by
\[ v_n = {\frac {\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2} + 1\right)}} \] Assuming that \(n\) is positive,
\[ \begin{aligned} \log{v_n} &= \log {\frac {\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2} + 1\right)}} \\ &= \frac {n}{2} \log {\pi} + \log {\frac {1}{\Gamma \left(\frac {n}{2} + 1\right)}} \end{aligned} \]
The limit of the above is \[ \begin{aligned} \lim_{n \to \infty} \log {v_n} &= \lim_{n \to \infty} \left[ \frac {n}{2} \log {\pi} + \log {\frac {1}{\Gamma \left(\frac {n}{2} + 1\right)}} \right] \\ &= \lim_{n \to \infty} \left[ \frac {n}{2} \log {\pi} - \log {\Gamma \left(\frac {n+2}{2}\right)} \right] \\ &= \lim_{n \to \infty} \left[ n \log {\pi} \left( \frac{1}{2} - \frac{\log {\Gamma \left(\frac {n+2}{2}\right)}}{ n \log {\pi} } \right) \right] \end{aligned} \] Then, by applying the product rule:
\[ \begin{aligned} \lim_{n \to \infty} \log {v_n} &= \log{\pi} \left( \lim_{n \to \infty} n \right) \left( \lim_{n \to \infty} \left[ \frac{1}{2} - \frac{\log {\Gamma \left(\frac {n+2}{2}\right)}}{ n \log {\pi} } \right] \right) \\ &= \log{\pi} \cdot \infty \left(\frac{1}{2} - \infty \right) \\ &= - \infty \end{aligned} \]
Therefore,
\[ \lim_{n \to \infty}{v_n} = 0 \]